¿Qué tan lejos puedes ver un meteoro?
>Recibo un correo electrónico.
La mayoría hace preguntas de varios tipos, la mayoría de las cuales son bastante sencillas de responder (de hecho, muchas de ellas podrían responderse buscando en Google, pistas indirectas). Pero a veces recibo una pregunta que es más difícil de responder, o incluso una que me he preguntado acerca de mí mismo pero que nunca llegué a resolver.
Así que estaba bastante intrigado cuando recibí una pregunta del Bad Reader Dean Lewis sobre los meteoros. Durante la lluvia de meteoros de las Perseidas en 2018, estaba lejos de su familia, separados por unos 1.000 kilómetros. Si veía un meteoro, ¿era posible que pudieran ver el mismo desde su lugar más distante?
¡La respuesta corta es sí! La respuesta larga es… matemáticas. Matemáticas divertidas y geniales.
Y viendo cómo, cuando se publique este artículo, la lluvia de meteoros Gemínidas anual de 2018 alcanza su punto máximo esta noche, creo que es apropiado resolver esto.
Astronomía Crash Course: Meteoros, Meteoroides y Meteoritos, ¡Oh Dios mío!
Si la Tierra fuera perfectamente plana, entonces, en principio, se podría ver un meteoro hasta cualquier borde de la Tierra. Mientras esté por encima del suelo, aunque sea un poquito, entonces su línea de visión alcanza cada centímetro cuadrado del planeta de su lado, por lo que cada meteoro es visible para todos. En realidad, el aire no es perfectamente transparente, por lo que a cierta distancia estás mirando a través de tanta suciedad que no puedes ver nada.
Sin embargo, la Tierra no es plana. ¡Seriamente! Es redondo. Y la atmósfera lo rodea como un caparazón, adelgazándose con la altura y eventualmente desapareciendo; esa altura depende de tu definición de espacio. Sin embargo, podemos hacer un poco de trampa ya que conocemos la ciencia: los meteoritos como los de las lluvias tienden a arder a unos 100 kilómetros sobre el suelo. Esa altura depende de muchas cosas, incluido el tamaño meteoroides (los trozos sólidos de escombros interplanetarios que atraviesan el espacio) son, qué tan rápido se mueven, en qué ángulo ingresan a la atmósfera, etc. Pero llamémoslo 100 km.
Lo más cerca que puede estar un meteoro de ti es si estás directamente debajo de él, y luego está a 100 km en línea recta (en tu cenit). Si se quema más lejos del cenit, entonces debe estar más lejos de ti. Lo más lejos que se puede ver un meteoro, es lógico, es si está exactamente en el horizonte.
La geometría se ve así (nota: NO a escala):
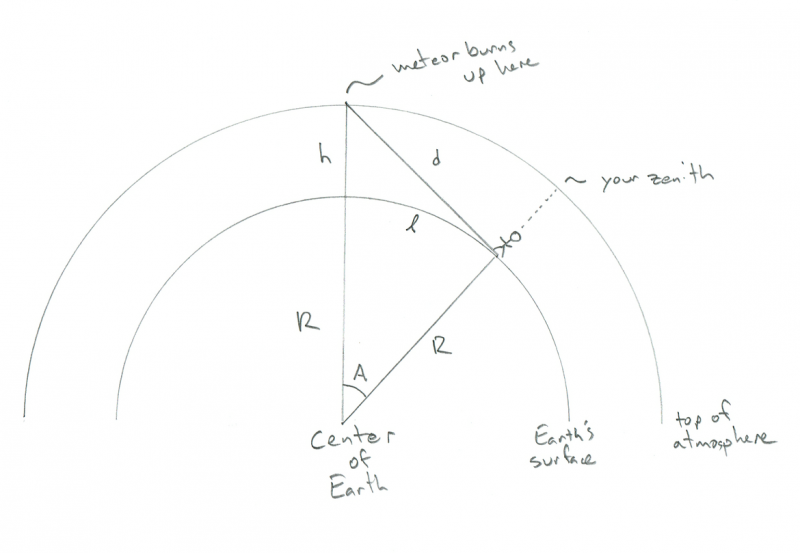
Esquema que muestra la geometría de un observador que observa cómo se quema un meteoro. Crédito: Phil Plait
Puedes ver la pequeña figura humana de pie en la superficie de la Tierra curva, digamos que eres tú, con la atmósfera (también curva) sobre ellos. En este diagrama, R es el radio de la Tierra (6,4000 km), h es la altura a la que se quema el meteoro (100 km) y d es la distancia entre usted y el meteoro. A es el ángulo entre tu posición en la Tierra y la posición del meteoro sobre ella, y la l cursiva (como en longitud) es la distancia que tendrías que caminar para que el meteoro esté directamente sobre tu cabeza (sé que parece algo extraño querer saber, pero tengan paciencia conmigo). Extrañamente, puedes calcular todo lo que necesitas aquí sin saber d, pero vamos, es genial saber qué tan lejos está el meteoro, ¿verdad?
La clave de todo esto es ver que el ángulo entre el meteoro, tú y el centro de la Tierra es un ángulo recto. Eso se debe a que el meteoro está en el horizonte tal como lo ve usted (o, si prefiere una jerga divertida, en la línea tangente del círculo interior donde R lo cruza). Eso hace que el triángulo sea un triángulo rectángulo, y si recuerdas las matemáticas de la escuela secundaria, eso significa que puedes encontrar todos los lados y ángulos.
Recordar el teorema de Pitágoras ? En un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados.*. En nuestro triángulo, la hipotenusa es R + h, y los otros lados son R y d.
Entonces
(R + h)2= d2+ R2
o, multiplicando el lado izquierdo (use FRUSTRAR ):
R2+ 2Rh + h2 = d2+ R2
verdaderas memorias de una película internacional de asesinos
Resuelve d para ver qué tan lejos está el meteoro de ti. Tenga en cuenta que R2 está en ambos lados, así que cancélelos para obtener
D2= 2Rh + h2
O
d = raíz cuadrada (2Rh + h2)
Bueno, ¡conocemos todos esos números! Plug-n-chug, bebé:
d = raíz cuadrada (2 x 6,400 x 100 + 10,000) = 1,136 km
¡Ajá! Esto significa que si ves un meteoro en el horizonte, ¡está a más de 1.100 kilómetros de distancia! Eso es un largo camino, y técnicamente lo más lejos que puedes ver un meteoro desde el suelo.
Ahora busquemos la l cursiva. Primero necesitamos conocer el ángulo A. Eso requiere algo de trigonometría. Hay un montón de identidades trigonométricas puedes usar para resolver esto, pero mi favorito†es que en un triángulo rectángulo, el seno de un ángulo es la longitud del lado opuesto dividida por la longitud de la hipotenusa. Entonces, si obtenemos esa razón, podemos tomar el seno inverso (o arcoseno) para obtener el ángulo.
pecado (A) = d / (R + h)
asi que
A = sin-1(d / R + h)
Plug-n-chug de nuevo, y obtengo A = 10 °. ¡Esa es una porción decente de la superficie de la Tierra!
Y ahora podemos poner la l en cursiva. Hay 360 ° alrededor de la Tierra, y la circunferencia de la Tierra es 2 x pi x radio = 40,192 km, por lo que hay
40192 km / 360 ° = 112 kilómetros por grado
lo que significa, a su vez, 10 ° = 1.120 kilómetros. Eso está bastante cerca de d, lo cual no es demasiado sorprendente. Los dibujos son exagerados, pero en realidad la capa de aire que nos cubre es pequeña en comparación con el tamaño de la Tierra. Si hiciera los dibujos a escala, verías que dy l son bastante parecidos en longitud.
Bien, entonces, ¿por qué estoy tan acalorado y molesto por encontrarlo? ¡Por la pregunta original! Si olvidaste después de todas esas matemáticas, ¿qué tan lejos pueden estar dos personas y seguir viendo el mismo meteoro?
Bueno, en ese caso el meteoro estaría directamente entre ellos, y en cada uno de sus respectivos horizontes. Esa geometría se ve así:
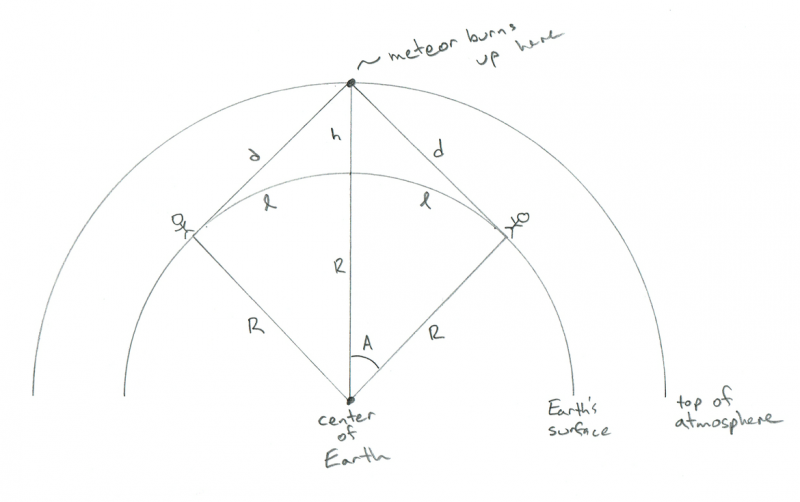
Esquema que muestra la geometría de dos observadores que miran un meteoro ardiendo exactamente entre ellos. Crédito: Phil Plait
AHA! ¡Ahora ves por qué lo quiero! ¡La distancia entre las dos personas es de solo 2 x l! Entonces ahora tenemos la respuesta:
Para que dos personas vean el mismo meteoro, no pueden estar separados por más de 2 x 1120 = 2240 kilómetros. Por ejemplo, eso se acerca bastante a la distancia entre Washington, DC y Denver. Guau.
Por cierto, para un cambio de perspectiva (literalmente), esto significa que desde el punto de vista del meteoro, puede ver un tramo de la Tierra de 2.240 kilómetros de ancho (como en DC en el extremo este de la Tierra y Denver en el oeste). Eso es muy bonito.
Y eso nos lleva a la respuesta real a la pregunta de Dean: si estaba a 1.000 km de su familia, entonces sí, técnicamente podrían ver el mismo meteoro. ¿Qué hay sobre eso?
Ahora, esto nuevamente supone que el aire está perfectamente claro y todo eso, lo que en realidad es esencialmente imposible. Entonces, esta matemática representa una situación ideal (incluida la idea de que el meteoro está exactamente entre ellos).
Seamos más realistas. Digamos que el meteoro se quema en el cielo a una altitud de 45 ° sobre el horizonte para ambos observadores. ¿Qué tan lejos estarían el uno del otro? Bueno, nuevamente asumiendo que el meteoro está exactamente entre ellos, la geometría es más así:
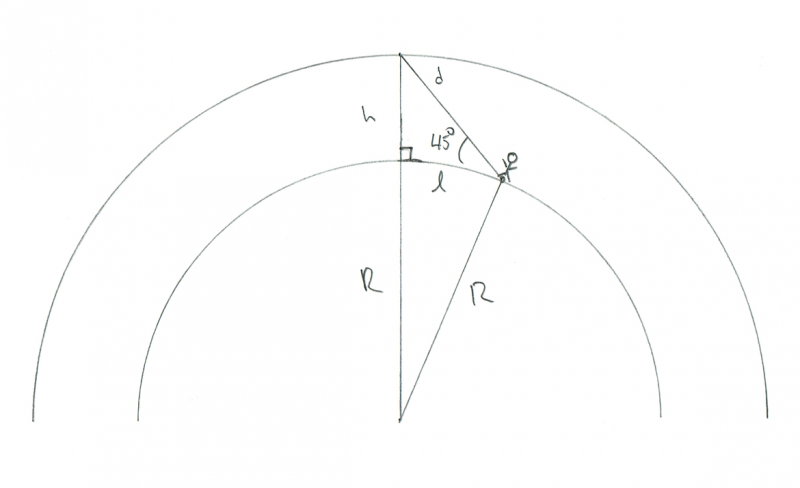
Esquema que muestra la geometría de un observador que observa un meteoro ardiendo a 45 ° sobre el horizonte. Crédito: Phil Plait
En realidad, esto es más difícil de resolver, pero conozco otro truco: si asumimos que l es pequeño, entonces la curvatura de la Tierra no será importante. Por ejemplo, si quiero saber la distancia entre dos árboles en mi jardín, no me importa que la Tierra sea curva. En una distancia tan pequeña, puedo asumir que es plano. Hagamos esa suposición aquí.
En ese caso, tenemos otro triángulo rectángulo, pero esta vez el ángulo recto es el que está debajo del meteoro. Incluso lo etiqueté en el diagrama con la pequeña notación cuadrada. Entonces, si ese es un ángulo de 90 °, y nuestro ángulo con el meteoro es de 45 °, entonces el último ángulo (desde el meteoro hasta el observador) también es de 45 °. Eso significa que debe ser un triángulo isósceles, ¡así que l y h son iguales! Como sabemos que h es 100 km, l también debe hacerlo.
Y eso significa que la distancia entre nuestros dos observadores es el doble, o 200 km.
Por cierto, en este caso la distancia al meteoro es de unos 141 km. Lo dejo confirmando eso como un ejercicio para el lector.
En principio, esto significa que si sabe qué tan alto en el horizonte está un meteoro y la altitud a la que se quemó, puede calcular su distancia (o si conoce la distancia, puede obtener su altura). Sin embargo, esa trigonometría es bastante complicada y creo que ya te he dicho suficientes matemáticas por hoy.
Pero es genial pensar que un poco de matemáticas de la escuela secundaria puede tener una aplicación tan divertida. Y admito que es poético y romántico saber que, siempre que la separación no sea demasiado lejana, es posible compartir el ver una estrella fugaz con otra persona. Qué hermoso pensamiento.
* En El mago de Oz , el espantapájaros se equivocó después tiene cerebro.
† De curso Tengo una identidad trigonométrica favorita. ¿Lo que es tuyo?